Les régulateurs PID sont le plus souvent utilisés pour influencer certaines grandeurs de mesure. En tant que régulateurs 3 en 1 intelligents, ils font quotidiennement leurs preuves dans de nombreux systèmes industriels et régulent très précisément la consigne. Chez nous, vous découvrirez les données et les faits les plus importants concernant la régulation PID.
Un régulateur PID numérique peut être programmé et paramétré de manière universelle grâce à un microprocesseur intégré. Il fonctionne de manière proportionnelle, intégrative et différentielle (PID), l'intensité des différentes composantes étant adaptée au système de régulation. Cela se fait par le dimensionnement des paramètres de régulation
Le principe d'un régulateur PID est relativement simple à expliquer. Qu'il s'agisse par exemple d'un régulateur de température PID ou d'un régulateur d'humidité PID, le régulateur tente toujours d'ajuster une certaine grandeur de régulation à la valeur de consigne à l'aide de la valeur réelle. Pour cela, le régulateur P renforce l'écart de régulation, la composante I augmente son taux de modulation en présence d'un écart de régulation et le régulateur D s'oppose au mouvement de la valeur réelle. Si toutes les composantes ne sont pas nécessaires à la régulation, elles peuvent être désactivées. Selon l'application, elles sont alors nommées régulateur PI, régulateur P, régulateur PD ou régulateur I.
Pour la plupart des applications, la structure PID présente la meilleure allure de régulation. Ainsi, les régulateurs PID compacts sont très répandus dans le domaine de la régulation de température, ils permettent également le raccordement direct de sondes à résistance et de thermocouples. Certaines grandeurs de régulation nécessitent la désactivation de certaines composantes, dont, entre autres, la vitesse et le débit.
La composante P réagit très rapidement et renforce la différence de régulation, son écart de régulation permanent a un effet négatif. Le paramètre de régulation responsable est la bande proportionnelle Xp. Plus la valeur de Xp est faible, plus le régulateur est rapide et plus l'écart de réglage est faible. Mais l'ensemble du système a de plus en plus tendance à osciller.
La composante I élimine l'écart de régulation. Si le temps d'intégrale Tn est réglé plus petit, le régulateur augmente plus rapidement son taux de modulation et agit plus rapidement contre l'écart de réglage. Toutefois, un réglage trop faible entraîne également un comportement oscillant.
La composante D s'oppose au mouvement de la valeur réelle. Pour un régulateur de chauffage, cela signifie que la part diminue lorsque la valeur réelle augmente et qu'elle augmente lorsque la valeur réelle diminue. Le comportement décrit a un effet d'amortissement. Le paramètre responsable est le temps de dérivation Tv. Plus Tv est élevé, plus l'effet décrit est important.
Le comportement des systèmes asservis dépend toujours du point de fonctionnement. Pour l'optimisation, le système doit être placé dans un état de fonctionnement pour lequel des paramètres de régulation favorables sont attendus ultérieurement. Par exemple, un four est chargé avant l'optimisation, tandis qu'une diminution doit être générée pour un chauffe-eau instantané. Si une valeur cible doit être définie lors de l'optimisation, celle-ci se situe plus tard dans la plage de travail.
S'il existe des systèmes/boucles de régulation comparables, les paramètres de commande qui y sont utilisés peuvent être utilisés à titre d'essai. Si cette approche ne permet pas d'atteindre l'objectif, l'une des méthodes d'optimisation suivantes peut être utilisée.
Méthode d'oscillation suivant Ziegler et Nichols
Cette méthode est utilisée pour les systèmes asservis relativement rapides. Pour la préparation, la structure P est paramétrée et un XP relativement grand est réglé. Une consigne dans la zone de travail ultérieure est définie dans la figure ci-dessous.
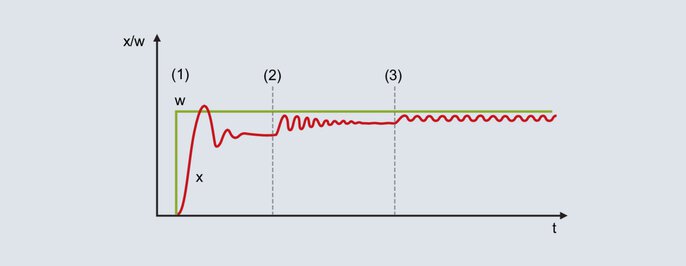
Figure 52: Évolution de la valeur de consigne et de la valeur réelle lors de l'utilisation de la méthode d'oscillation
Avec la plage proportionnelle réglée relativement grande, la valeur réelle atteint la valeur finale avec une faible tendance à l'oscillation [figure 52 (1)]. En raison de l'absence de structure I, il existe un écart de réglage permanent.
La valeur réelle augmente et se dirige vers la valeur finale avec une plus grande tendance à l'oscillation. Dans certaines circonstances, la bande proportionnelle est réduite plusieurs fois jusqu'à ce que la valeur réelle oscille en permanence (figure 52 [3]). La bande proportionnelle nécessaire pour ce comportement est appelée XPk (Xp critique) et doit être déterminée le plus précisément possible (ne pas réduire Xp par trop grands pas).
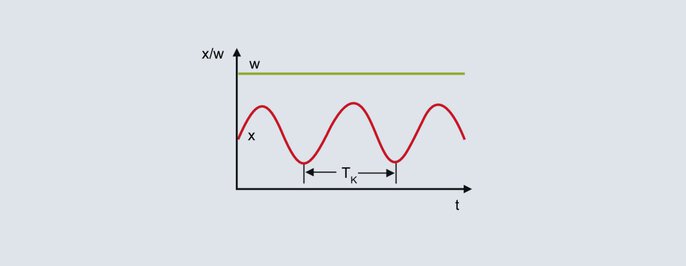
Durée critique de la période
La deuxième grandeur caractéristique du procédé est déterminée à partir de l'oscillation continue de la valeur réelle dans la figure supérieure, avec la durée de période critique TK. La durée de période critique TK (en secondes) résulte par exemple de l'intervalle de temps entre deux valeurs minimales. XPk et TK sont insérés dans le tableau suivant pour la structure de régulation souhaitée :
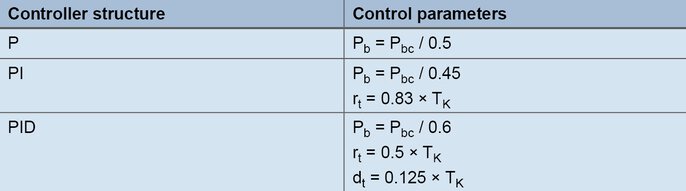
Formules de réglage selon la méthode des oscillations
Méthode de saut de réglage suivant Chien, Hrones et Reswic
Cette méthode permet de déterminer les paramètres de régulation de manière relativement rapide, même pour les systèmes asservis inertes. La méthode est utilisée pour les systèmes de 2ème ordre et plus et offre la particularité de distinguer les formules pour le comportement de commande et de perturbation. Pour les formules empiriques, le coefficient de transfert du système asservi, le temps de retard et le temps de compensation sont déterminés à partir de la réponse à un échelon.
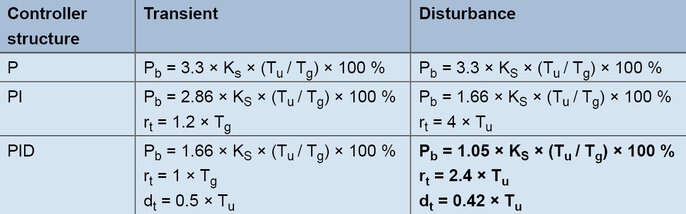
Formules de création selon la réponse à 1 échelon
Exemple :
Un régulateur numérique avec structure PID doit être utilisé pour un four de laboratoire. L'objectif est d'obtenir un bon comportement face aux perturbations, les valeurs de consigne typiques sont de 200 °C. En mode manuel, le taux de modulation est augmenté progressivement jusqu'à obtenir une valeur réelle légèrement inférieure à la valeur de consigne ultérieure (il faut à chaque fois attendre les processus de compensation). Par exemple, avec un taux de modulation de 60 %, on obtient une température de 180 °C. En partant de 60 %, le taux de modulation est augmenté par paliers jusqu'à 80 % et la valeur réelle est enregistrée.
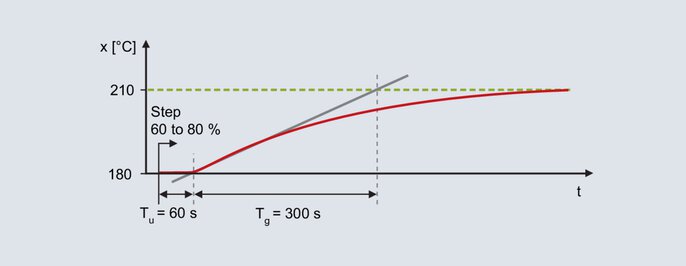
Réponse à 1 échelon du four du laboratoire
La réponse à un échelon est déterminée à l'aide de la tangente au point d'inflexion : Temps mort Tu = 60 s, temps de compensation Tg = 300 s. Le coefficient de transfert du système asservi est obtenu en divisant la variation de la valeur réelle par le saut du taux de modulation.
Equation 22
En utilisant les formules empiriques, on obtient les paramètres suivants pour le comportement perturbateur :
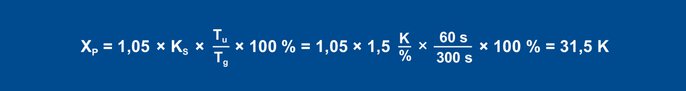
Equation 23
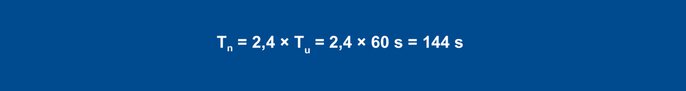
Equation 24
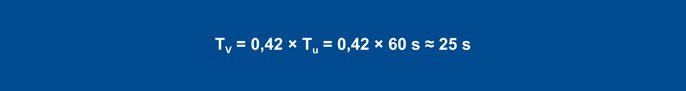
Equation 25
Le saut du taux de modulation doit être effectué dans la zone du point de fonctionnement ultérieur. La hauteur du saut doit être choisie de manière à ce que l'évolution de la valeur réelle puisse être évaluée. Après avoir défini le saut du taux de modulation, on attend la valeur finale de la valeur réelle ; la méthode selon la vitesse de montée offre une alternative permettant de gagner du temps.
Procédure selon la vitesse de montée
En ce qui concerne la définition de l'échelon, la procédure est la même que pour la procédure selon la réponse à un échelon. Avant le saut, on définit un taux de modulation avec lequel la valeur réelle est légèrement inférieure à la valeur de consigne utilisée ultérieurement.
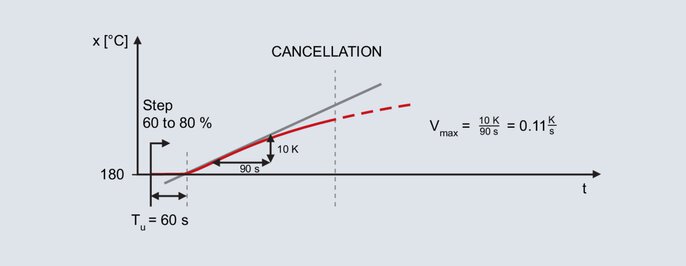
Evolution de la valeur réelle lors du procédé selon la vitesse de montée
L'échelon est à nouveau défini pour le four de laboratoire déjà mentionné ; le point de fonctionnement ultérieur est également de 200 °C. En définissant un taux de modulation de 60 % en mode manuel, on obtient une valeur réelle de 180 °C. Le taux de modulation est augmenté par sauts à 80 %.
Une fois l'échelon prédéfini, la valeur réelle augmente au bout d'un certain temps. L'enregistrement s'effectue jusqu'à ce que la valeur réelle présente sa pente maximale. Pour ce procédé également, la tangente du point d'inflexion est tracée et le temps mort est déterminé. La deuxième grandeur caractéristique est la vitesse maximale de montée, celle-ci correspond à la pente de la tangente de retournement. La vitesse maximale de montée est déterminée par un triangle de pente sur la tangente du point d'inflexion.
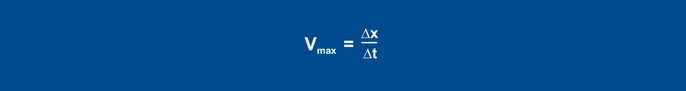
Equation 26
Les valeurs obtenues Vmax (0,11 K/s) et Tu (60 s) sont utilisées dans les formules suivantes :
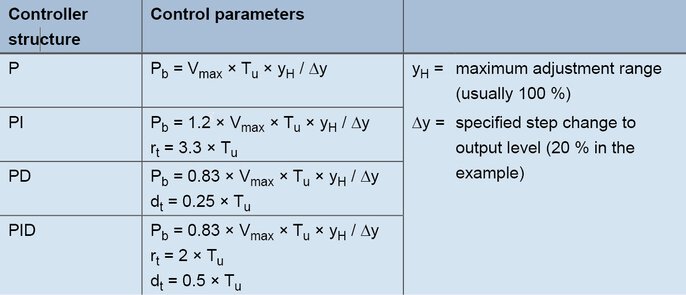
Formules de réglage en fonction de la vitesse de montée
Pour un régulateur PID, les valeurs sont obtenues à l'aide des formules suivantes :
Equation 27
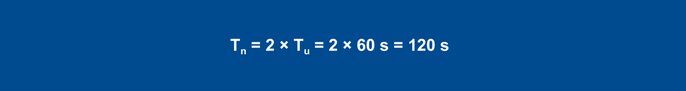
Equation 28
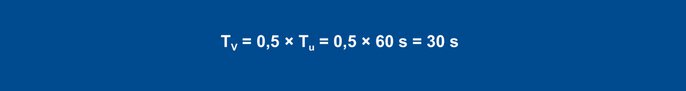
Equation 29
Méthode empirique de détermination des paramètres de régulation
Cette méthode permet de déterminer successivement des réglages favorables pour les composantes P, D et I. En partant de l'état initial (taux de modulation 0 %), on donne toujours la valeur de consigne typique ; c'est pourquoi cette méthode n'est applicable qu'aux systèmes asservis relativement rapides (par ex. systèmes asservis rapides en température et grandeurs réglées comme la vitesse ou le débit).
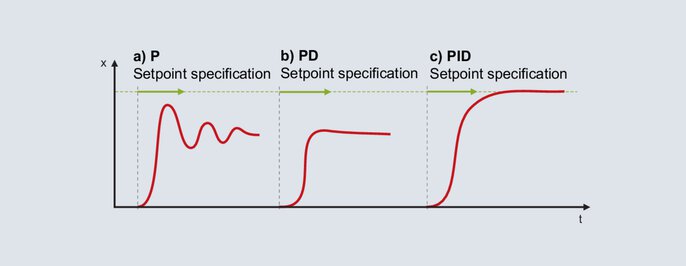
Réglage d'un régulateur PID selon la méthode empirique
Pour le régulateur numérique, la structure P est activée. La bande proportionnelle est réglée relativement grande (le dimensionnement dépend du système de régulation) et la valeur de consigne est donnée dans la zone de travail ultérieure. La valeur réelle évoluera paresseusement vers la valeur finale et il en résultera un écart de régulation relativement important. Par la suite, la valeur de consigne est définie avec une plage proportionnelle XP de plus en plus petite. L'objectif est un Xp pour lequel la valeur réelle atteint sa valeur finale stable après deux ou trois oscillations complètes (figure 56a). Pour un démarrage amorti, la structure passe de P à PD. En commençant par un petit réglage pour le temps de dérivation, la définition de la valeur de consigne s'effectue avec des Tv de plus en plus grandes. Si la valeur réelle atteint sa valeur finale avec une oscillation aussi petite que possible, on est en présence d'un Tv favorable (figure 56b).
Nota : Dès que le régulateur règle le taux de modulation sur 0 %, même une seule fois, au démarrage, le Tv est réglé trop grand.
Le passage à la structure PID active la composante I. Le temps de réglage Tn est généralement réglé favorablement avec la valeur quadruple du téléviseur déterminé précédemment. La figure 56c montre le comportement pour un réglage Tn = 4 × Tv.
Pour certains systèmes, toutes les parties ne peuvent pas être activées. Si, avec une structure P, on obtient déjà un comportement instable pour de grands réglages de XP, ni la structure P ni la structure D ne peuvent être utilisées. Le régulateur I est alors utilisé.
Si l'optimisation du régulateur P a réussi, mais que l'introduction de la composante D rend la boucle de régulation instable, la structure PI est utilisée.
L'application des méthodes d'optimisation présentées ci-dessus entraînera très probablement un comportement de régulation stable, mais pas optimal. Une optimisation manuelle ultérieure permet d'améliorer encore le résultat de la régulation. Si le comportement d'un régulateur PID peut être attribué à l'une des courbes 62b à 62e, vous trouverez ci-dessous des indications pour une optimisation supplémentaire.
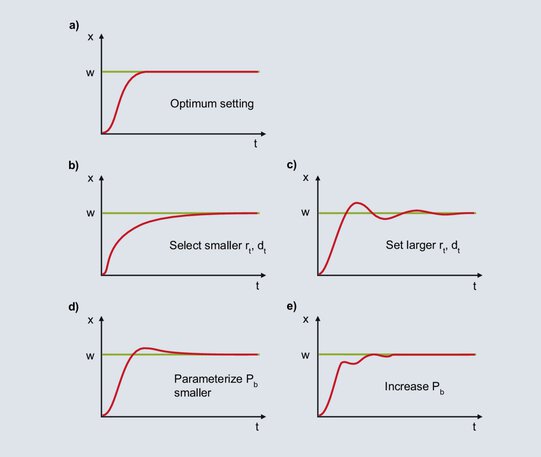
Figure 62: Remarques sur l’optimisation d’un régulateur PID
Le diagramme montre un comportement optimal pour un régulateur PID.
Une fois la valeur de consigne définie, la valeur réelle augmente fortement jusqu'à ce que la bande proportionnelle soit atteinte. Lorsque la valeur réelle atteint la bande proportionnelle, la composante P est réduite et la composante I assure la régulation sur la valeur de consigne. L'augmentation de la part I se fait lentement en raison du réglage relativement grand de Tn et l'écart de réglage est éliminé lentement. Pour une intégration plus rapide, Tn doit être réglé plus bas ; Tv est également réduit en fonction du rapport Tv/Tn = 1/4.
Lorsque la valeur réelle entre dans la bande proportionnelle, la composante I augmente le taux de modulation. L'augmentation se poursuit jusqu'à ce que la valeur réelle atteigne la consigne. Dans le cas représenté, la composante I accumule trop de taux de modulation jusqu'à l'élimination de l'écart de réglage, la valeur réelle dépasse la consigne. En présence d'un écart de réglage négatif, le taux de modulation est réduit trop rapidement, la valeur réelle passe en dessous de la consigne, etc. L'oscillation symétrique de la valeur réelle autour de la consigne indique que Tn est réglé sur une valeur trop faible. Il faut augmenter Tn et Tv également en fonction du rapport Tv / Tn = 1/4.
La composante I est formée depuis l'entrée de la valeur réelle dans la bande proportionnelle jusqu'à l'élimination de l'écart de réglage. En raison du réglage élevé de Xp, la composante I commence à former le taux de modulation dès que l'écart de réglage est important. Grâce à l'écart de réglage important au début, la composante I forme son taux de modulation relativement rapidement. Lorsque l'écart de réglage est éliminé, la composante I est trop importante, la valeur réelle dépasse la consigne. Avec un réglage plus faible pour Xp, la composante I ne commence à établir son taux de modulation qu'en cas d'écart de réglage plus faible, donc plus lentement. La suroscillation unique représentée est moins probable.
Avec un XP réglé trop bas, le taux de modulation de la composante P est réduit juste avant que la consigne ne soit atteinte. Lorsque la valeur réelle entre dans la bande proportionnelle, la composante P est très fortement réduite et la valeur réelle diminue. En raison de l'écart de réglage plus important, le taux de modulation augmente et la valeur réelle augmente. Dans la bande proportionnelle, de petites modifications de la valeur réelle entraînent de grandes modifications du taux de modulation, ce qui se traduit par une forte tendance aux oscillations. L'augmentation de la bande proportionnelle permet d'obtenir une stabilisation.
